Guaranteed Discovery of Controllable Latent States with Multi-Step Inverse Models
AC-State: Principled Representation Learning for Reinforcement Learning
The AC-State algorithm discovers a latent representation of a system from a sequence of sensory observations and actions taken by an agent interacting in the system, while requiring no external supervision (such as rewards or labels). This consists of predicting actions from observations with the smallest possible representation. This representation provably captures all of the information which is necessary for controlling the agent while discarding all irrelevant or distracting details. Previous approaches either fail to capture the full state or fail to ignore irrelevant information. We demonstrate this on a robot arm where we are able to recover the position of the arm using only a high-resolution video and recorded actions, while ignoring complex background distractors.
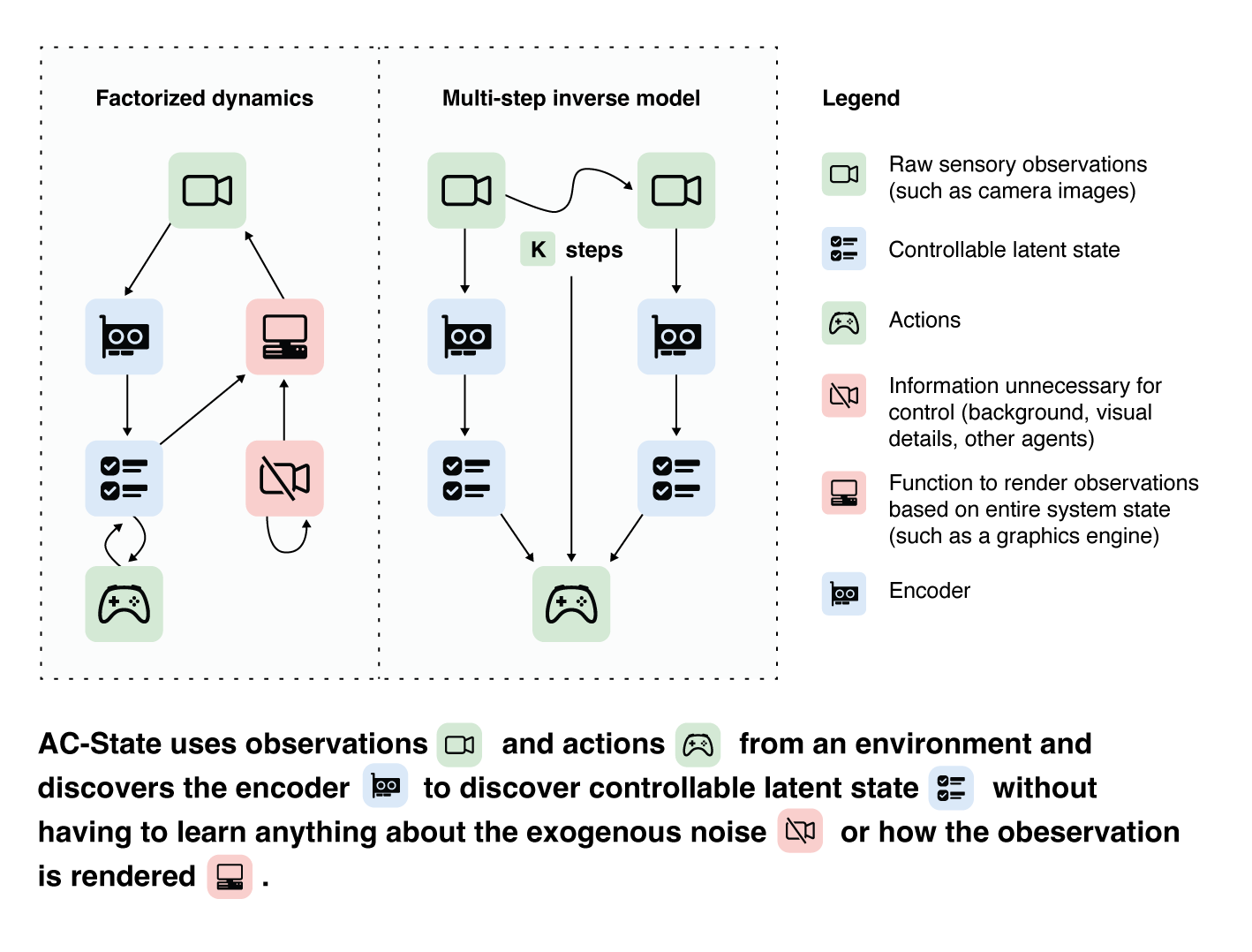
Background: Why do we need latent state decoding?
A person walking along a city street who tries to model all aspects of the world would quickly be overwhelmed by a multitude of shops, cars, and people moving in and out of view, following their own complex and inscrutable dynamics. Exploration and navigation in such an environment is an everyday task, requiring no vast exertion of mental resources. Is it possible to turn this fire hose of sensory information into a minimal latent state which is necessary and sufficient for an agent to successfully act in the world? We formulate this question concretely, and propose the Agent-Controllable State Discovery algorithm (AC-State), which has theoretical guarantees and is practically demonstrated to discover the minimal controllable latent state which contains all of the information necessary for controlling the agent, while fully discarding all irrelevant information. This algorithm consists of a multi-step inverse model (predicting actions from distant observations) with an information bottleneck. AC-State enables localization, exploration, and navigation without reward or demonstrations. We demonstrate the discovery of controllable latent state in three domains: localizing a robot arm with distractions (e.g., changing lighting conditions and background), exploring in a maze alongside other agents, and navigating in the Matterport house simulator.
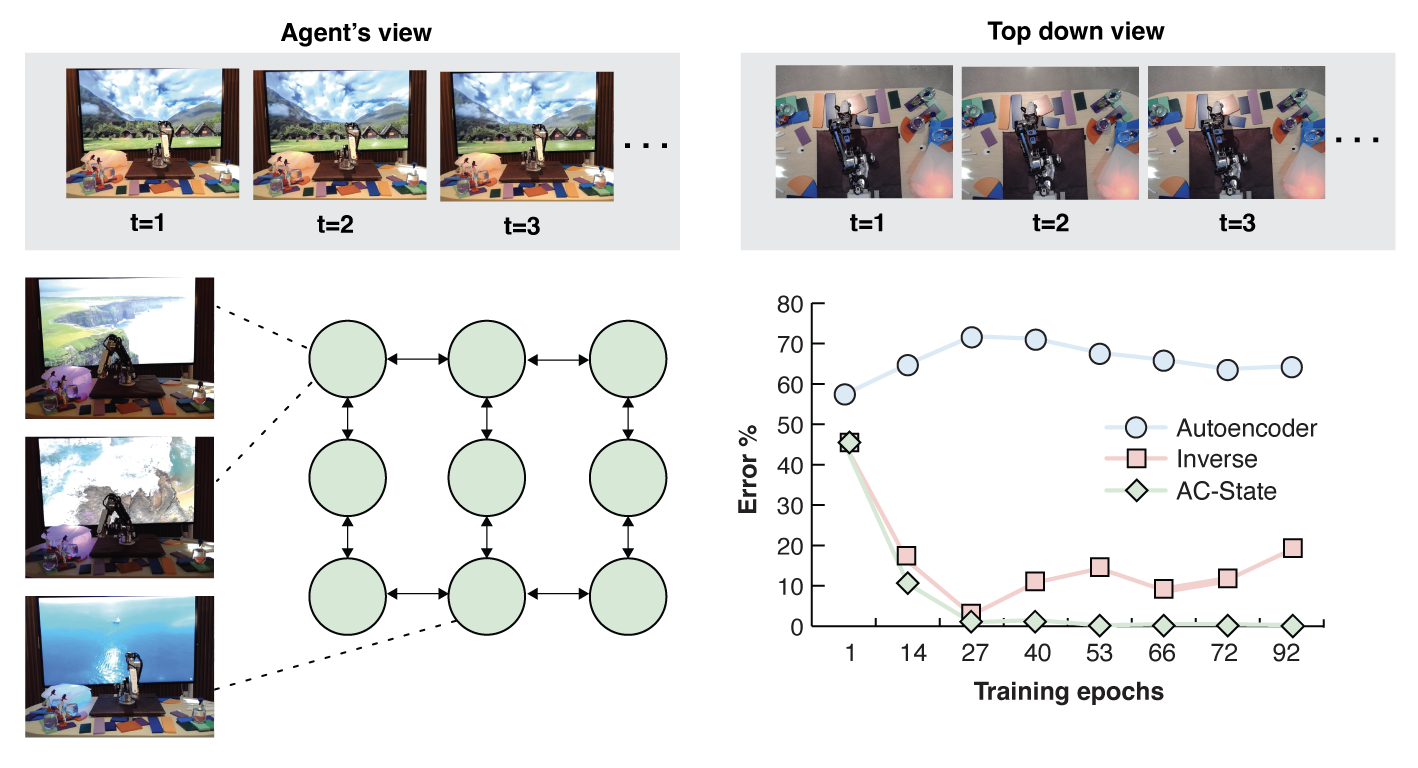
A real robot arm moving between nine positions (left). The quality of controllable latent state dynamics learned by AC-State is better than one-step inverse models and autoencoders (bottom right).

AC-State discovers controllable latent state in a visual robotic setting with temporally correlated distractors: a TV, flashing lights, and drinking bird toys (top left). We visualize the learned latent state by training a decoder to reconstruct the observation (top right). This shows that AC-State learns to discover the robot arm's position while ignoring the background distractors (videos in supplement). In co-occurrence histograms (bottom), autoencoders fail (bottom left), one-step inverse models fall prey to the same counterexample in theory and in experiment (bottom center), and AC-State discovers a perfect controllable latent state (diagonal histogram, bottom right).
Experiments
- AC-State learns the controllable latent state of a real robot from a high-resolution video of the robot with rich temporal background structure (a TV playing a video, flashing lights, dipping birds, and even people) dominating the information in the observed dynamics
- multiple mazes and functionally identical agents where only one agent is controlled. AC-State only learns about the controlled agent while ignoring others, enabling the solution of a hard maze-exploration problem
- AC-State learns controllable latent state in a house navigation environment where the observations are high-resolution images and the camera's vertical position randomly oscillates, showing that the algorithm is invariant to exogenous viewpoint noise which radically changes the observation.
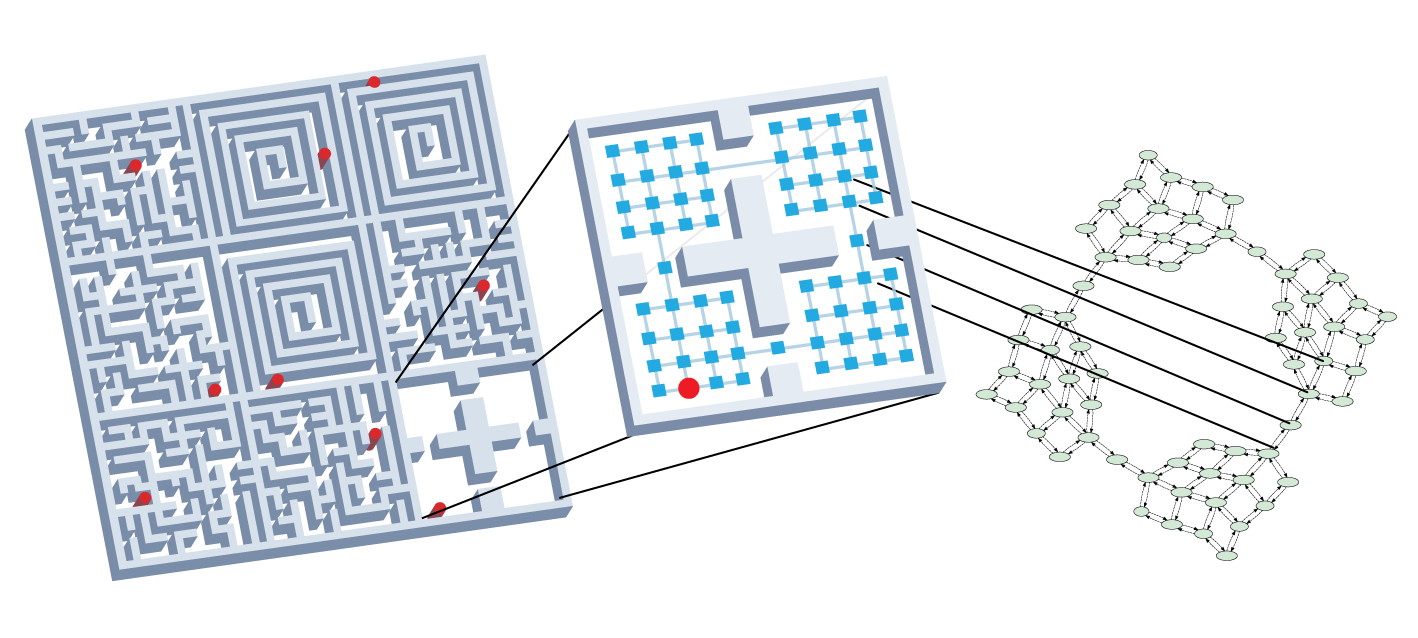
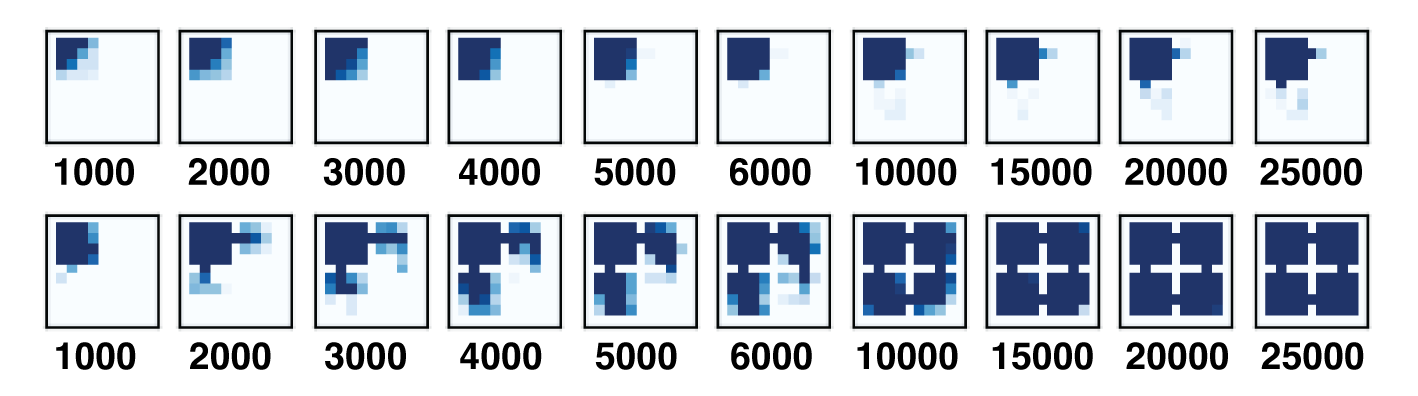
We study a multi-agent world where each of the nine mazes has a separately controlled agent. Training AC-State with the actions of a specific agent discovers its controllable latent state while discarding information about the other mazes (top). In a version of this environment where a fixed third of the actions cause the agent's position to reset to the top left corner, a random policy fails to explore, whereas planned exploration using AC-State reaches all parts of the maze (bottom).
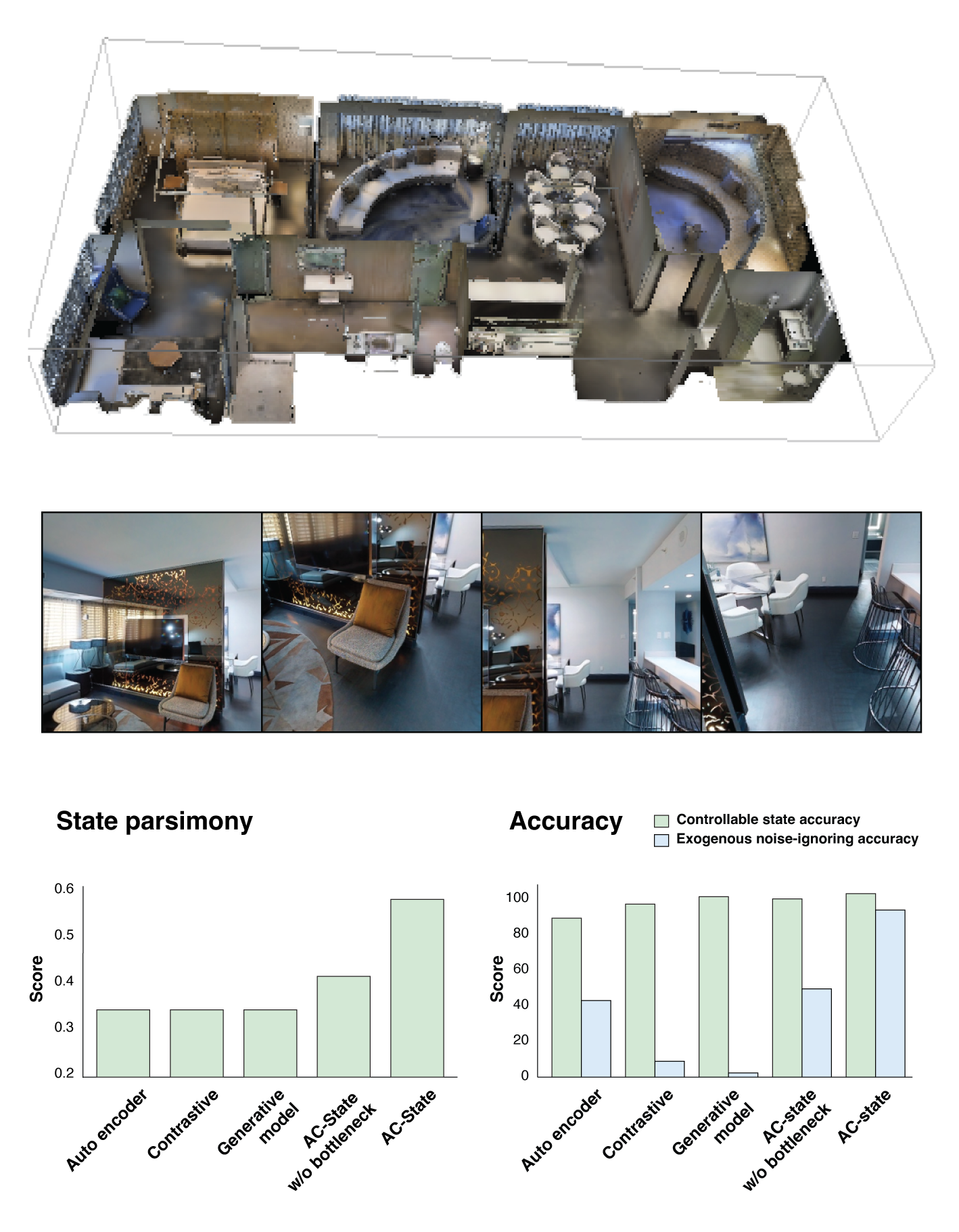
We evaluate AC-State in a house navigation environment (top), where the agent observes high resolution images of first-person views where the vertical position of the camera is random exogenous noise (center). The algorithm discovers a controllable latent state which is parsimonious (bottom left). AC-State captures the position of the agent in the house and discards information about the position of the camera (bottom right). The baselines we consider capture the controllable latent state but fail to discard the exogenous noise.
Summary
- AC-State reliably discovers controllable latent state across multiple domains. The vast simplification of the controllable latent state discovered by AC-State enables visualization, exact planning, and fast exploration. The field of self-supervised reinforcement learning particularly benefits from these approaches, with AC-State useful across a wide range of applications involving interactive agents as a self contained module to improve sample efficiency given any task specification. As the richness of sensors and the ubiquity of computing technologies (such as virtual reality, internet of things, and self-driving cars) continues to grow, the capacity to discover agent-controllable latent states enables new classes of applications.
- Conditioning trajectories on a future desired state alongside previously-encountered states yields a goal-reaching method.